Test de Student sur deux échantillons (two sample t-test)
Introduction
Le test t de Student sur deux échantillons indépendants est un test paramétrique permettant de déterminer s'il existe une différence statistiquement significative entre deux échantillons (et donc généralisable à la population).
Pour des explications plus détaillées, n'hésitez pas à consulter mes notes de première année.
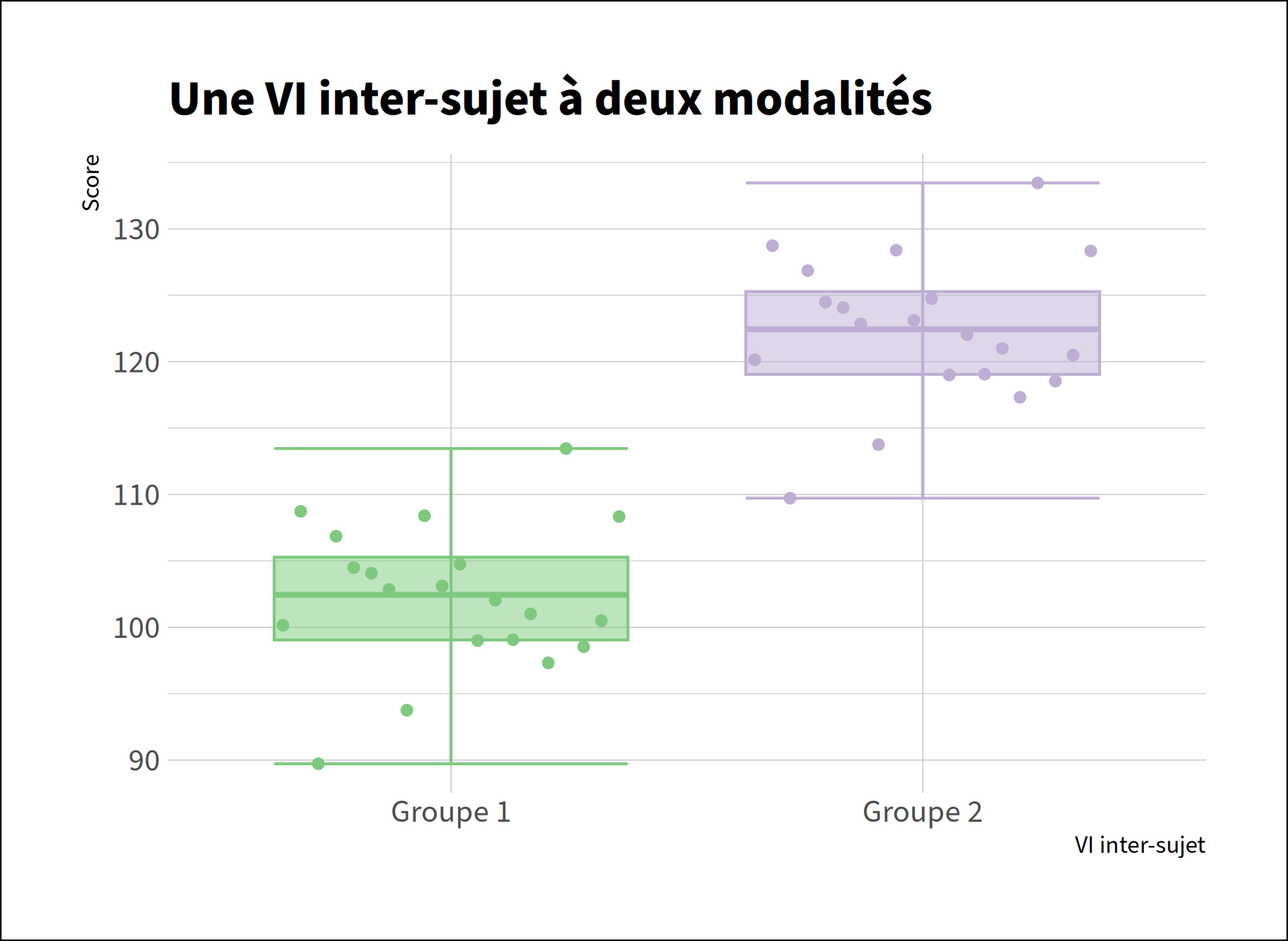
Conditions d'application
Conditions d'application
Pour pouvoir être appliqué, ce test nécessite que les échantillons soient issus de distributions normales et que leurs variances soient homogènes.
- Si les échantillons ne proviennent pas de distribution normales, il faut utiliser un test non-paramétrique. Dans ce cas, un test de Mann-Whitney.
- Si les variances ne sont pas homogènes, il faut utiliser une correction. Dans ce cas, la méthode de Welch.
Pour vérifier si les distributions sont normales, nous devons utiliser un test de Shapiro-Wilk:
# Soit y la variable dépendante et x la variable indépendante/manipulée
by(data$y, data$x, shapiro.test)
Pour vérifier si les variances sont homogènes, nous devons utiliser un test de Levene:
# Soit y la variable dépendante et x la variable indépendante/manipulée
library(car)
leveneTest(data$y ~ data$x)
Exécution du test
# Soit y la variable dépendante et x la variable indépendante/manipulée
t.test(data$y ~ data$x, var.equal=TRUE)
Taille d'effet
Comme nous pouvons le voir en regardant l'équation du t-test indépendant, la p-valeur dépend de la taille de l'échantillon. Plus la taille d'échantillon augmente, plus on risque de trouver une différence significative pour une différence en réalité très faible.
Pour remédier à cela, il est nécessaire de calculer la taille d'effet en utiliser le d de Cohen:
# Soit y la variable dépendante et x la variable indépendante/manipulée
library(effsize)
cohen.d(data$y ~ data$x)
Exemple
Voici nos données et notre fichier d'analyse:
| Fichiers |
|---|
| two-sample-t-test.csv |
| two-sample-t-test.R |
Commençons par activer les librairies nécessaires dans R:
library(car)
library(effsize)
Puis, importons nos données:
df <- read.csv("two-sample-t-test.csv")
df$groupe <- as.factor(df$groupe)
Nous pouvons maintenant visualiser nos données dans un diagramme en boîtes à moustache:
boxplot(
score ~ groupe, data=df,
xlab="Groupe", ylab="Score",
main="Two sample t-test",
col="steelblue"
)
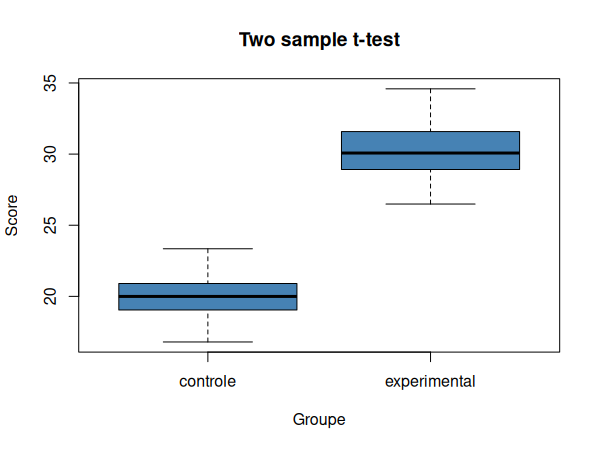
Vérifions maintenant les conditions d'application, tout d'abord la normalité des distributions:
by(df$score, df$groupe, shapiro.test)
| W | p | |
|---|---|---|
| Contrôle | 0.99626 | 0.9954 |
| Expérimental | 0.98395 | 0.2661 |
Nous pouvons donc conclure que les deux échantillons sont issus de distributions normales.
Puis, nous vérifions l'homogénéité des variances:
leveneTest(score ~ groupe, data=df)
| Df | F | Pr(>F) | |
|---|---|---|---|
| group | 1 | 0.0216 | 0.8833 |
| 198 |
Nous pouvons donc conclure que les deux variances sont homogènes.
Puisque les conditions d'applications sont satisfaites, nous pouvons réaliser un t-test indépendant:
t.test(score ~ groupe, data=df, var.equal=TRUE)
| t | df | p |
|---|---|---|
| -74.41 | 198 | < 2.2e-16 *** |
Nous pouvons donc conclure que les deux échantillons sont issus de populations différentes, c'est-à-dire qu'il existe une différence significative entre les scores des deux échantillons. Il ne reste maintenant plus qu'à calculer la taille d'effet. Pour cela, nous utilisons le d de Cohen:
cohen.d(score ~ groupe, data=df)
| d | size | 95% CI |
|---|---|---|
| -10.5231 | large | lower -11.597511 upper -9.448685 |
La taille d'effet étant grande, nous pouvons conclure qu'il existe une grande différence significative entre le groupe contrôle et le groupe expérimental (t(198) = -74.41, p<.001, d = -10.52).