Analyse de variance à un facteur (one-way ANOVA)
Introduction
L'analyse de variance (ANOVA) de Fisher à un facteur est un test paramétrique permettant de déterminer si plus de deux échantillons sont issus de populations différentes.
Pour des explications plus détaillées, n'hésitez pas à consulter mes notes de première année.
Conditions d'application
Conditions d'application
Pour pouvoir être appliqué, ce test nécessite que les échantillons soient issus de distributions normales et que leurs variances soient homogènes.
- Si les échantillons ne proviennent pas de distribution normales, il faut utiliser un test non-paramétrique. Dans ce cas, un test de Kruskal-Wallis.
- Si les variances ne sont pas homogènes, il faut utiliser une correction. Dans ce cas, la correction de Welch.
Pour vérifier si les distributions sont normales, nous devons utiliser un test de Shapiro-Wilk:
# Soit y la variable dépendante et x le facteur
by(data$y, data$x, shapiro.test)
Pour vérifier si les variances sont homogènes, nous devons utiliser un test de Levene:
# Soit y la variable dépendante et x le facteur
library(car)
leveneTest(data$y ~ data$x)
Exécution du test
# Soit y la variable dépendante et x le facteur
m <- aov(data$y ~ data$x)
summary(m)
Cependant, ce résultat ne nous donne pas d'informations suffisantes. En effet, il nous informe uniquement qu'il existe une différence statistiquement significative entre certaines modalités de notre facteur, alors que nous cherchons à savoir pour quelles modalités il y a un effet. Pour cela, nous devons réaliser un test post-hoc, ici un test HSD de Tukey:
TukeyHSD(m)
Taille d'effet
Comme pour le test t de Student, il est nécessaire de calculer la taille d'effet pour savoir si celui-ci est important ou non. Pour ce faire, nous devons utiliser le coefficient η2 (êta carré):
library(lsr)
etaSquared(m)
Exemple
Voici nos données et notre fichier d'analyse:
| Fichiers |
|---|
| one-way-anova.csv |
| one-way-anova.R |
Commençons par activer les librairies nécessaires dans R:
library(car)
library(lsr)
Puis, importons nos données:
df <- read.csv("one-way-anova.csv")
df$groupe <- as.factor(df$groupe)
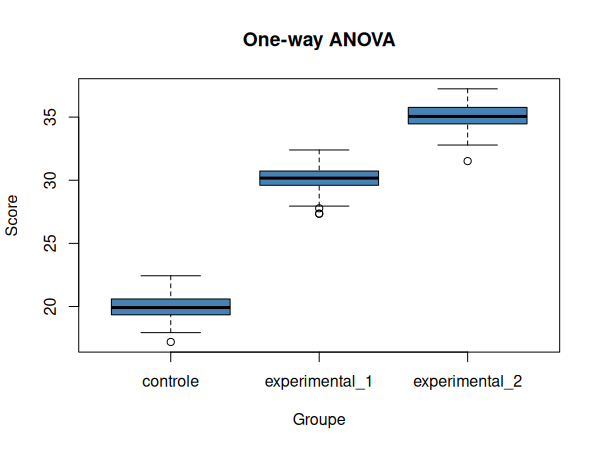
Nous pouvons maintenant visualiser nos données dans un diagramme en boîtes à moustache:
boxplot(
score ~ groupe, data=df,
xlab="Groupe", ylab="Score",
main="One-way ANOVA",
col="steelblue"
)
Vérifions maintenant les conditions d'application, tout d'abord la normalité des distributions:
by(df$score, df$groupe, shapiro.test)
| W | p | |
|---|---|---|
| Contrôle | 0.99626 | 0.9954 |
| Expérimental 1 | 0.98395 | 0.2661 |
| Expérimental 2 | 0.97944 | 0.1202 |
Nous pouvons donc conclure que tous les échantillons sont issus de distributions normales.
Puis, nous vérifions l'homogénéité des variances:
leveneTest(score ~ groupe, data=df)
| Df | F | Pr(>F) | |
|---|---|---|---|
| group | 2 | 0.0618 | 0.9401 |
| 297 |
Nous pouvons donc conclure que les variances sont homogènes.
Puisque les conditions d'applications sont satisfaites, nous pouvons réaliser une ANOVA à un facteur de classification:
m <- aov(score ~ groupe, data=df)
summary(m)
| Df | Sum Sq | Mean Sq | F value | Pr(>F) | |
|---|---|---|---|---|---|
| groupe | 2 | 11823 | 5912 | 6467 | <2e-16 *** |
| Residuals | 297 | 271 | 1 |
Nous constatons donc qu'il y a un effet. Cependant, nous souhaitons savoir entre quels groupes est visible cet effet. Pour cela, nous réalisons un test post-hoc:
TukeyHSD(m)
| $groupe | diff | p adj |
|---|---|---|
| Expérimental 1-Contrôle | 10.148151 | 0 |
| Expérimental 2-Contrôle | 15.079685 | 0 |
| Expérimental 2-Expérimental 1 | 4.931534 | 0 |
Grâce à ces résultats, nous pouvons conclure qu'il existe une différence significative entre chaque échantillon. Il ne nous reste maintenant plus qu'à mesurer la taille de cette différence en utilisant le coefficient η2:
etaSquared(m)
| eta.sq | eta.sq.part | |
|---|---|---|
| groupe | 0.9775544 | 0.9775544 |
Puisque η2 > 0.14, nous pouvons affirmer que la taille d'effet est grande. Nous concluons donc qu'il existe une grande différence significative entre les groupes (F(2,297) = 6467, p<.001, η2 = 0.98).