Analyse de variance mixte (mixed ANOVA)

Introduction

L'analyse de variance (ANOVA) mixte est un test paramétrique permettant de déterminer s'il existe une différence significative entre plusieurs échantillons en présence d'un facteur intra-sujet (temporel).

Conditions d'application

Pour pouvoir être appliqué, ce test nécessite que les échantillons soient issus de distributions normales, que la sphéricité des variances soit respectée (variances similaires entre les différents points de mesure), et que la variances des facteurs inter-sujets soient homogènes.

Information

Nous n'avons pas besoin de vérifier la sphéricité des variances, car le test est effectué directement dans la fonction de l'ANOVA, et la correction de Greenhouse-Geisser sera appliquée en cas de problème.

Exécution du test

Syntaxe R

# Soit y la variable dépendante, 
# x le facteur inter-sujet,
# ID l'identifiant de chaque participant.e.x,
# et time le facteur temporel (intra-sujet)
library(rstatix)
m <- anova_test(
    data=data,
    dv=y,
    wid=ID,
    within=time,
    between=x
)
get_anova_table(m, correction="GG")

Taille d'effet

Information

La taille d'effet est automatiquement calculée par la fonction que nous utilisons pour calculer l'ANOVA. Nous n'avons donc pas besoin de la calculer.

Exemple

Voici nos données et notre fichier d'analyse:

Fichiers
mixed-anova.csv
mixed-anova.R

Commençons par activer les librairies nécessaires dans R:

Activation des librairies

library(rstatix)
library(RcmdrMisc)

Puis, importons nos données:

Importation des données

df <- read.csv("mixed-anova.csv")
df$groupe <- as.factor(df$groupe)
df$time <- as.factor(df$time)

Nous pouvons maintenant visualiser nos données dans un diagramme:

Diagramme des moyennes

plotMeans(
  df$score,
  df$time,
  df$groupe,
  xlab="Temps", 
  ylab="Score",
  legend.lab="Groupe"
)

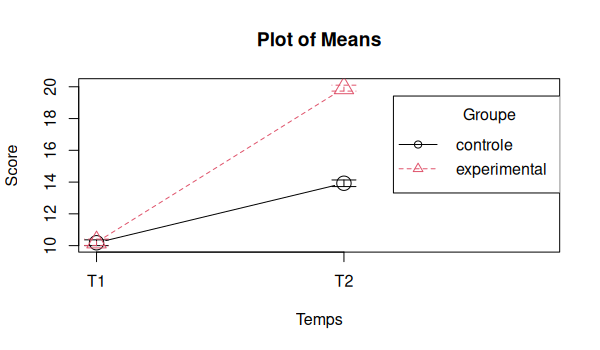
Réalisons maintenant notre ANOVA:

ANOVA mixte

m <- anova_test(
  data=df,
  dv=score,
  wid=ID,
  within=time,
  between=groupe
)
get_anova_table(m, correction="GG")

Effect	Dfn	Dfd	F	p	ges
groupe	1	198	222.377	3.30e-34	0.377
time	1	198	1302.620	5.04e-89	0.752
groupe:time	1	198	255.501	1.76e-37	0.373

Le facteur inter-sujet groupe, le facteur intra-sujet time, ainsi que l'interaction entre les deux ont un effet significatif sur la variable dépendante score, et que cet effet est grand.

Nous pouvons donc conclure qu'il existe une grandes différence significative entre les différents groupes (F_(1,198) = 222.38, p<.001, η²_G = 0.38), entre les différentes mesures (F_(1,198) = 1302.62, p<.001, η²_G = 0.75), ainsi qu'un effet d'interaction entre le facteur groupe et le facteur de temps (F_(1,198) = 255.5, p<.001, η²_G = 0.37).