Test U de Mann-Whitney (Wilcoxon rank sum test with continuity correction)
Introduction
Le test U de Mann-Whitney est l'équivalent non-paramétrique du test t de Student sur deux échantillons.
Pour des explications plus détaillées, n'hésitez pas à consulter mes notes de première année.
Conditions d'application
Conditions d'application
Pour pouvoir être appliqué, ce test nécessite que les échantillons ne soient pas issues de distributions normales.
- Si les distributions sont normales, il faut absolument utiliser un test paramétrique. Dans ce cas, un t-test à deux échantillons indépendants.
Pour vérifier si les distributions sont normales, nous devons utiliser un test de Shapiro-Wilk:
# Soit y la variable dépendante et x la variable indépendante/manipulée
by(data$y, data$x, shapiro.test)
Exécution du test
# Soit y la variable dépendante et x la variable indépendante/manipulée
wilcox.test(data$y ~ data$x)
Exemple
Voici nos données et notre fichier d'analyse:
| Fichiers |
|---|
| mann-whitney-u-test.csv |
| mann-whitney-u-test.R |
Importons nos données:
df <- read.csv("mann-whitney-u-test.csv")
df$groupe <- as.factor(df$groupe)
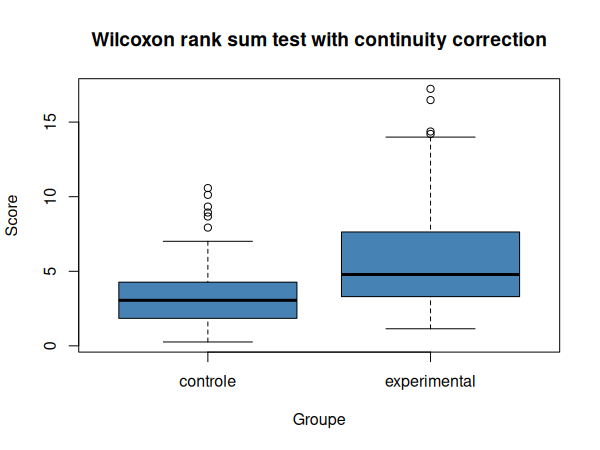
Nous pouvons maintenant visualiser nos données dans un diagramme en boîtes à moustache:
boxplot(
score ~ groupe, data=df,
xlab="Groupe", ylab="Score",
main="Wilcoxon rank sum test with continuity correction",
col="steelblue"
)
Vérifions maintenant la normalité des distributions:
by(df$score, df$groupe, shapiro.test)
| W | p | |
|---|---|---|
| Contrôle | 0.92354 | 2.181e-05 |
| Expérimental | 0.91107 | 4.871e-06 |
Nous pouvons donc conclure que les deux échantillons ne sont pas issus de distributions normales. Nous ne pouvons donc pas effectuer de test paramétrique.
Réalisons maintenant notre test non-paramétrique:
wilcox.test(score ~ groupe, data=df)
| W | p-value |
|---|---|
| 2839 | 1.299e-07 *** |
Nous pouvons donc conclure que les deux échantillons sont issus de populations différentes, c'est-à-dire qu'il existe une différence significative entre les scores des deux échantillons (W = 2839, p<.001).