Test de Friedman (Friedman rank sum test)

Introduction

Le test de Friedman est l'équivalent non-paramétrique de l'analyse de variance à mesures répétées.

Conditions d'application

Pour pouvoir être appliqué, ce test nécessite que les échantillons ne soient pas issues de distributions normales.

Si les distributions sont normales, il faut absolument utiliser un test paramétrique. Dans ce cas, un l'ANOVA à mesures répétées.

Pour vérifier si les distributions sont normales, nous devons utiliser un test de Shapiro-Wilk:

Syntaxe R

# Soit y la variable dépendante et time le facteur temporel (intra-sujet)
by(df$y, data$time, shapiro.test)

Exécution du test

Syntaxe R

# Soit y la variable dépendante, 
# ID l'identifiant de chaque participant.e.x 
# et time le facteur temporel (intra-sujet)
friedman.test(data$y, data$time, data$ID)

Nous devons ensuite réaliser un test post-hoc, pour connaître entre quelles mesures cette différence s'exprime. Ici, nous utilisons des tests de Wilcoxon sur mesures pairées:

Syntaxe R

pairwise.wilcox.test(data$y, data$time, paired=TRUE, p.adjust.method="bonf")

Exemple

Voici nos données et notre fichier d'analyse:

Fichiers
friedman-rank-sum-test.csv
friedman-rank-sum-test.R

Commençons par activer les librairies nécessaires dans R:

Activation des librairies

library(RcmdrMisc)

Puis, importons nos données:

Importation et recodage des données

data <- read.csv("friedman-rank-sum-test.csv")
df <- data.frame(
    ID=rep(data$ID, 3),
    score=c(data$T1, data$T2, data$T3),
    time=factor(rep(c("T1", "T2", "T3"), each=100))
)

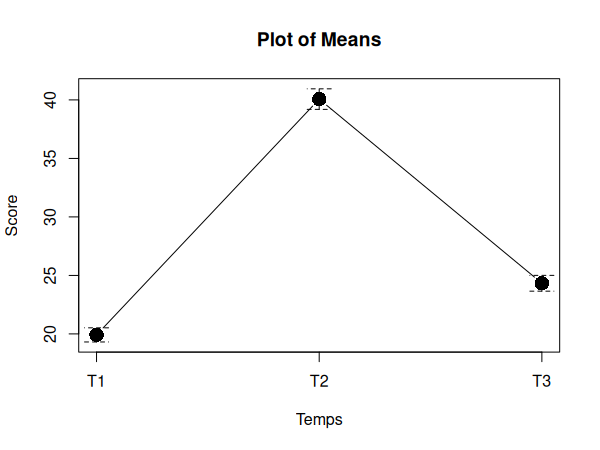
Nous pouvons maintenant visualiser nos données dans un diagramme:

Diagramme des moyennes

plotMeans(df$score, df$time, xlab="Temps", ylab="Score")

Vérifions maintenant la normalité des distributions:

Test de normalité de Shapiro-Wilk

by(df$score, df$time, shapiro.test)

	W	p
T1	0.97295	0.03732
T2	0.97514	0.05536
T3	0.9877	0.4864

Nous pouvons donc conclure que certaines mesures ne sont pas distribuées normalement. Nous ne pouvons donc pas utiliser de test paramétrique.

Effectuons maintenant notre test non-paramétrique:

Test de Friedman

friedman.test(df$score, df$time, df$ID)

χ²	df	p-value
121.94	2	< 2.2e-16 ***

Nous pouvons conclure qu'il y a un effet. Il ne nous reste maintenant plus qu'à chercher entre quelles mesures s'exprime cet effet:

Test post-hoc

pairwise.wilcox.test(df$score, df$time, paired=TRUE, p.adjust.method="bonf")

	T1	T2
T2	< 2e-16	-
T3	0.00015	7.1e-16

Il existe donc une différence significative entre toutes les mesures.

Nous pouvons donc conclure qu'il existe une différence significative entre nos mesures (χ²₍₂₎ =121.94, p<.001).