Régression linéaire simple
Introduction
La régression linéaire simple permet de tester l'effet d'un prédicteur (variable indépendante) sur une variable dépendante dans un modèle linéaire.
Bases théoriques
La régression permet d'aller au-delà de la corrélation puisqu'elle suppose que la variable indépendante permet de prédire la variable dépendante. Cependant, étant donné son utilisation qui se fait dans des designs observationnels — dans lesquels il n'est pas possible de manipuler la VI — il n'est pas possible d'émettre de causalité sur la base de l'analyse de régression.
L'équation de la régression est la suivante:
Avec:
- y la variable dépendante
- β0 l'intercept (ou ordonnée à l'origine)
- β1 la pente de la régression linéaire
- x le prédicteur (ou variable indépendante)
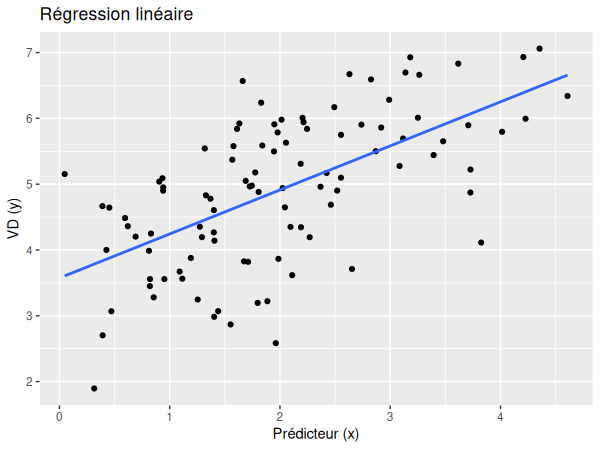
Si nous essayons de représenter la régression à l'aide d'un graphique, nous obtenons donc approximativement le schéma suivant:
Application
# Soit y la variable dépendante et x le prédicteur
m <- lm(data$y ~ data$x)
summary(m)
Conditions d'application
Note
Pour la régression, les conditions d'application ne peuvent être vérifiées qu'après la réalisation du modèle linéaire.
Conditions d'application
Pour pouvoir être utilisée, la régression linéaire simple requiert:
- La linéarité du modèle.
- La distribution normale des résidus.
- L'homoscédasticité (constance de la variance des résidus à tous les niveaux du prédicteur).
- L'absence de valeurs extrêmes.
- Pour vérifier la linéarité du modèle, nous utilisons un graphique des résidus par rapport aux valeurs ajustées.
- Pour vérifier la distribution normale des résidus, nous utilisons un graphique Q-Q.
- Pour vérifier l'homoscédasticité, nous utilisons un graphique de localisation d'échelle.
- Enfin, pour tester l'absence de valeurs extrêmes, nous utilisons un graphique des résidus par rapport au levier.
Il est possible de générer ces 4 graphiques pour le modèle de régression de la façon suivante:
# Soit m le modèle de régression linéaire
par(mfrow=c(1,1))
plot(m)
Interprétation
Comme pour la comparaison de groupes, la p-valeur nous renseigne sur la significativité. Si la p-valeur est plus grande que le seuil de significativité, cela signifie que notre prédicteur ne permet pas de prédire la variable dépendante. Si celle-ci est significative, le pente b nous indique à quelle augmentation moyenne de la VD est associée une augmentation d'une unité du prédicteur.
Taille d'effet
Pour la régression, le coefficient de détermination R2 est utilisé pour calculer la taille d'effet. Il est toujours compris entre 0 et 1 et représente le pourcentage de la variance de Y qui peut être expliquée par X. Il s'agit du carré de la corrélation entre les valeurs observées et prédites. En d'autres termes, si R2 = .4, cela signifie que 40% de la variance de Y peut être expliquée par X.
Dans le cas d'une régression simple — avec un seul prédicteur — nous utilisons le coefficient R2 mutiple.
Exemple
Voici nos données et notre fichier d'analyse:
| Fichiers |
|---|
| simple-linear-regression.csv |
| simple-linear-regression.R |
Commençons par activer les librairies nécessaires dans R:
library(ggplot2)
Puis, importons nos données:
df <- read.csv("simple-linear-regression.csv")
Nous pouvons maintenant visualiser nos données dans un diagramme:
ggplot(data=df, aes(x=predicteur, y=score)) +
geom_point() +
geom_smooth(method=lm, se=F) +
ggtitle("Simple linear model") +
xlab("Prédicteur") +
ylab("Score")

Réalisons maintenant notre régression:
m <- lm(score ~ predicteur, data=df)
Nous devons maintenant vérifier les suppositions de notre modèle de régression:
par(mfrow=c(1,1))
plot(m)
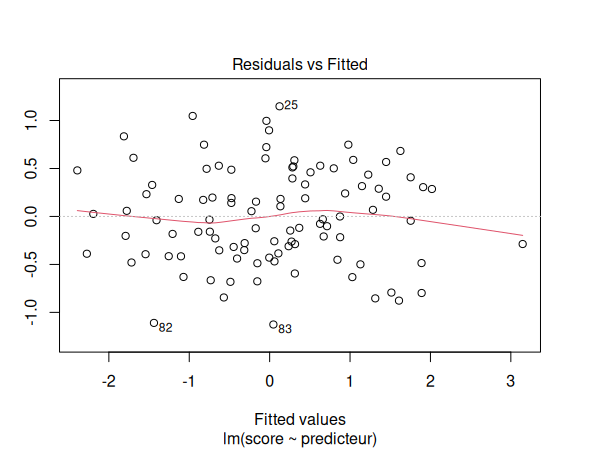
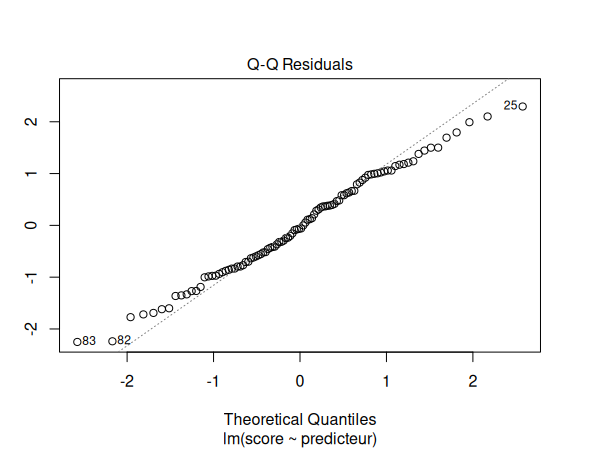
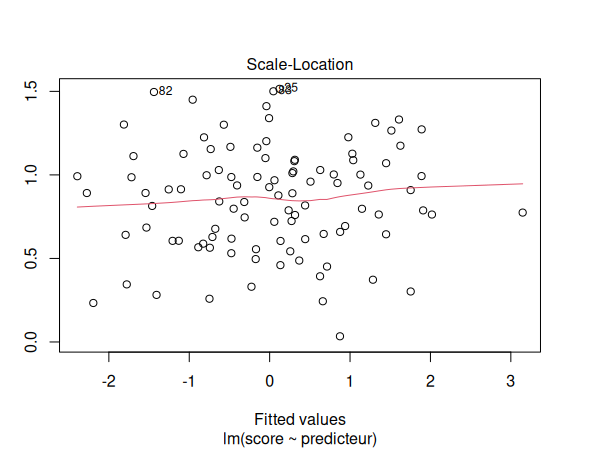
Les suppositions semblent être respectées. Nous pouvons donc interpréter nos résultats:
summary(m)
| Estimate | Std. Error | t value | p | |
|---|---|---|---|---|
| (Intercept) | 0.02051 | 0.05029 | 0.408 | 0.684 |
| predicteur | 1.08985 | 0.04995 | 21.817 | <2e-16 *** |
| F-statistic | p-value | Multiple R2 | Adjusted R2 |
|---|---|---|---|
| 476 | < 2.2e-16 | 0.8293 | 0.8275 |
Nous pouvons donc déduire de ces résultats qu'une augmentation d'une unité du prédicteur est associée à une augmentation moyenne de 0.90 unité du score (B = 0.90, t(98) = 21.82, p<.001, R2 = .829). Le prédicteur permet donc d'expliquer ~83% de la variance des scores.