Régression multiple
Introduction
La régression multiple permet de tester l'effet de plusieurs prédicteurs sur une variable dépendante dans un modèle linéaire.
Bases théoriques
Souvent, plusieurs facteurs ont une influence sur la variable dépendante. Or, il serait erroné de calculer une régression simple pour chacun de ces facteurs, puisque cela ne permettrait pas de tenir compte de l'influence des autres facteurs sur celui qui est analysé.
L'équation de la régression multiple est la suivante:
Avec:
- Y la variable dépendante
- β0 l'intercept (il n'y en a qu'un seul indépendamment du nombre de facteurs)
- β1X1 la pente du facteur 1
- β2X2 la pente du facteur 2
- βkXk les pentes des autres facteurs présents dans le modèle
Si nous essayons de représenter la régression multiple à l'aide d'un graphique, nous obtenons donc approximativement le schéma suivant (ici avec deux prédicteurs):
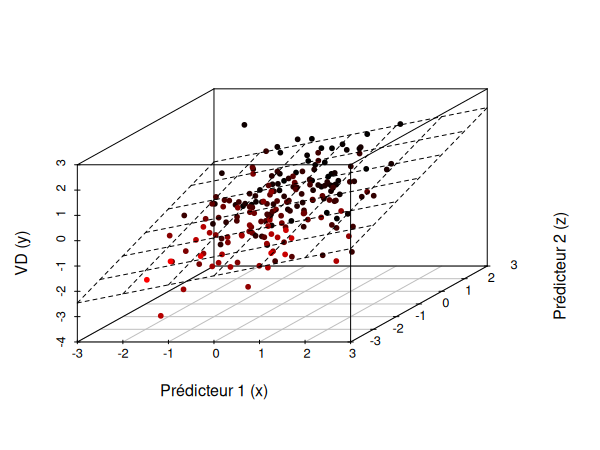
Ici, notre pente n'est en réalité plus une simple pente, il s'agit d'une figure géométrique appelée hyperplan. Un hyperplan est un sous-espace plat de dimension n-1: dans un espace en 2D, l'hyperplan est en 1D (par exemple dans le cas d'une régression linéaire simple). Dans un espace en 3D, l'hyperplan est en 2D, dans un espace en 4D l'hyperplan est en 3D, etc.
Application
# Soit y la variable dépendante et x1, x2 les prédicteurs
m <- lm(data$y ~ data$x1 + data$x2)
summary(m)
Conditions d'application
Conditions d'application
Pour pouvoir être utilisée, la régression linéaire multiple requiert:
- La linéarité du modèle.
- La distribution normale des résidus.
- L'homoscédasticité (constance de la variance des résidus à tous les niveaux du prédicteur).
- L'absence de valeurs extrêmes.
- L'absence de multicolinéarité (absence de corrélation forte entre 2 prédicteurs ou plus).
Comme pour la régression simple, nous pouvons vérifier les 4 premières suppositions de la façon suivante:
# Soit m le modèle de régression linéaire
par(mfrow=c(1,1))
plot(m)
Pour tester la multicolinéarité, nous utilisons le VIF (Variance Inflation Factor):
# Soit m le modèle de régression linéaire
library(car)
vif(m)
Coefficients standardisés
Les coefficients standardisés sont des coefficients de régression qui ont été convertis de façon à être mesurés en écarts-types. Lorsque l'on reporte les résultats, il est important de communiquer également les coefficients standardisés, puisque cela permet de comparer la force et la direction des différents coefficients.
Pour réaliser un modèle de régression multiple avec des coefficients standardisés:
# Soit y la variable dépendante et x1, x2 les prédicteurs
m <- lm(scale(data$y) ~ scale(data$x1) + scale(data$x2))
summary(m)
Taille d'effet
Dans le cadre d'une régression multiple, nous utilisons le R2 ajusté pour déterminer la part de la variance qui peut être expliquée par l'ensemble de nos prédicteurs.
Exemple
Voici nos données et notre fichier d'analyse:
| Fichiers |
|---|
| multiple-linear-regression.csv |
| multiple-linear-regression.R |
Commençons par activer les librairies nécessaires dans R:
library(car)
Puis, importons nos données:
df <- read.csv("multiple-linear-regression.csv")
Puisque nous avons 3 prédicteurs, nous ne pouvons pas représenter l'hyperplan graphiquement, puisque cela nécessiterait un graphique avec 4 axes différents (en 4D).
Réalisons maintenant notre régression:
m <- lm(
score ~ predicteur_1 + predicteur_2 + predicteur_3,
data=df
)
Nous devons maintenant vérifier les suppositions de notre modèle de régression:
par(mfrow=c(1,1))
plot(m)
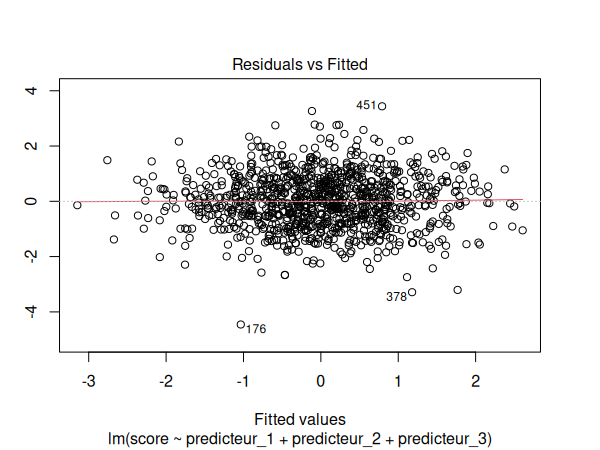
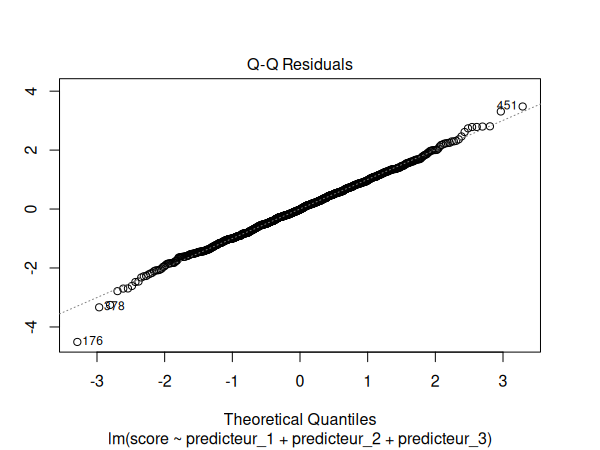
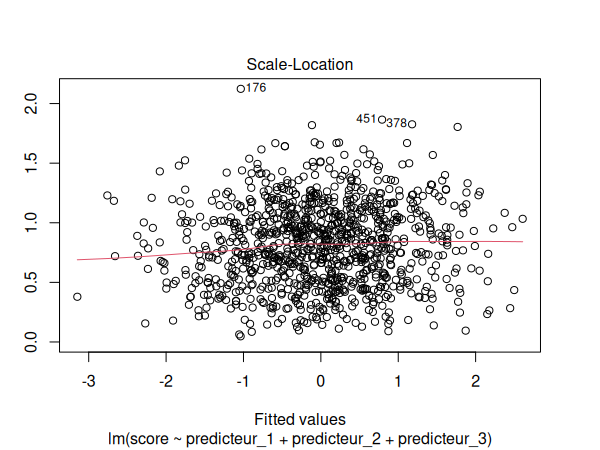
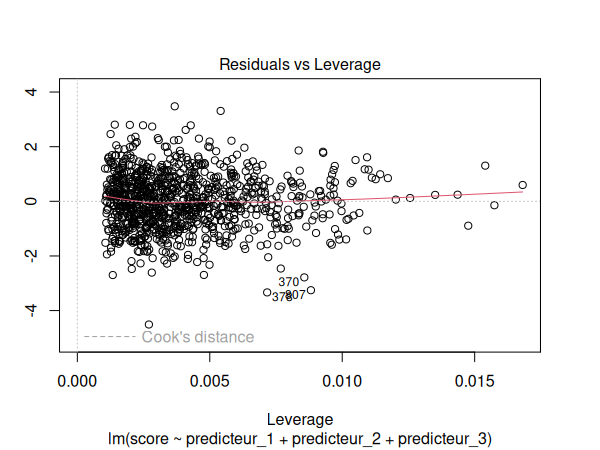
Puis nous testons notre modèle pour la multicolinéarité:
vif(m)
| predicteur_1 | predicteur_2 | predicteur_3 |
|---|---|---|
| 1.000931 | 1.002070 | 1.001448 |
Les suppositions semblent être respectées. Nous pouvons donc interpréter nos résultats:
summary(m)
| Estimate | Std. Error | t value | p | |
|---|---|---|---|---|
| (Intercept) | -0.001399 | 0.031331 | -0.045 | 0.964 |
| predicteur_1 | 0.587227 | 0.029759 | 19.733 | <2e-16 *** |
| predicteur_2 | 0.393529 | 0.030874 | 12.746 | <2e-16 *** |
| predicteur_3 | -0.529478 | 0.032376 | -16.354 | <2e-16 *** |
| F-statistic | p-value | Multiple R2 | Adjusted R2 |
|---|---|---|---|
| 286 | < 2.2e-16 | 0.4628 | 0.4612 |
Nous pouvons déduire de ces résultats que nos prédicteurs sont significatifs et qu'ils permettent d'expliquer ~46% de la variance des scores (F(3,996) = 286, p<.001, R2 = .461).
Une augmentation d'une unité du prédicteur 1 est associée à une augmentation moyenne de 0.59 unités du score (B = 0.59, p<.001). Une augmentation d'une unité du prédicteur 2 est associée à une augmentation moyenne de 0.39 unités du score (B = 0.39, p<.001). Une augmentation d'une unité du prédicteur 3 est associé à une diminution de 0.53 unité du score (B = -0.52, p<.001).
Nous pouvons maintenant calculer les coefficients standardisés:
m1 <- lm(
scale(score) ~ scale(predicteur_1) +
scale(predicteur_2) +
scale(predicteur_3),
data=df
)
summary(m1)
| Estimate | Std. Error | t value | p | |
|---|---|---|---|---|
| (Intercept) | 3.656e-17 | 0.02321 | 0.00 | 1 |
| predicteur_1 | 0.4585 | 0.02324 | 19.73 | <2e-16 *** |
| predicteur_2 | 0.2963 | 0.02325 | 12.75 | <2e-16 *** |
| predicteur_3 | -0.3801 | 0.02324 | -16.35 | <2e-16 *** |
Nous pouvons donc conclure que l'augmentation d'un écart-type du prédicteur 1 est associée à une augmentation de 0.46 écart-type du coefficient standardisé de la variable dépendante (B = 0.46, p<.001). Une augmentation d'un écart-type du prédicteur 2 est associée à une augmentation de 0.30 écart-type de la variable dépendante (B = 0.30, p<.001). Une augmentation d'un écart-type du prédicteur 3 est associée à une diminution de -0.38 écart-type de la variable dépendante (B = -0.38, p<.001).