Régression multiniveau (variations inter-/intra-groupe)
Bases théoriques
Dans la régression multiniveau effectuée précédemment, nous avions deux types d'effets: les effets fixes (communs à tout le monde) ainsi que les effets aléatoires (différents pour chaque groupe).
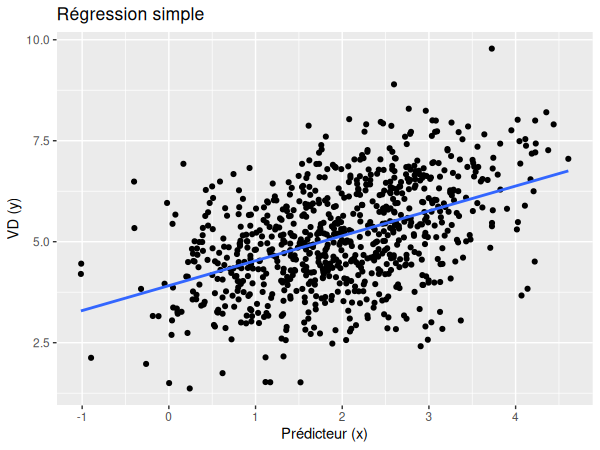
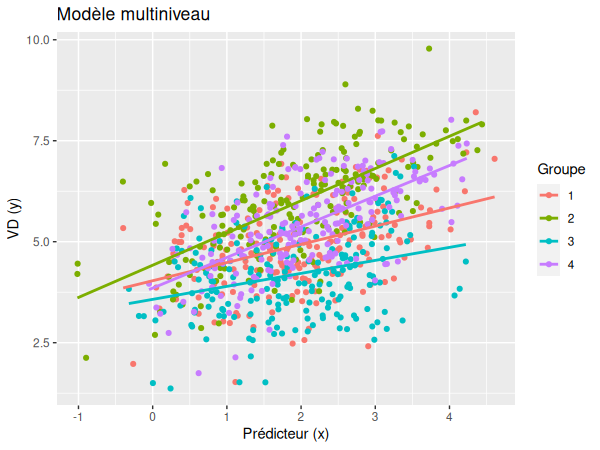
Cependant, dans un modèle multiniveau, il est nécessaire de séparer les effets de classe (ou effets de groupe) des effets indidivuels. Pour ce faire, nous devons d'abord calculer la moyenne des valeurs du prédicteur pour chaque groupe:

Puis soustaire cette moyenne à chacun des membre du groupe, et cela pour chaque groupe. Cela permet de calculer les effets individuels, puisqu'en effectuant la soustraction, cela débarasse les données de l'effet de groupe:

Note
Même si ce dernier graphique ressemble au graphique des effets aléatoires réalisé dans la régression multiniveau sans la séparation entre individu et classe, nous pouvons néanmoins remarquer que, dans ce graphique-ci, le prédicteur est centré, ce qui permet de visualiser uniquement les effets individuels, sans influence des effets de groupe.
Cependant, il existe également une pente commune à tous les individus. Il s'agit d'une pente fixe, dans laquelle on ne tient pas compte des différents groupes:

En séparant individu et contexte, nous obtenons donc 3 types d'effets:
- Les différences entre les classes (effet fixe car commun à toutes les classes).
- Les effets aléatoires.
- Les différences entre les individus (effet fixe car commun à tous les individus).
L'équation de cette nouvelle régression multiniveau est donc la suivante:
Avec:
- y la variable dépendante
- γ00 l'intercept fixe
- γ10 la pente fixe (moyenne de la classe)
- γ20 la pente fixe (écart individuel à la moyenne de la classe)
- r0j les intercepts aléatoires
- r1j les pentes aléatoires
- εji l'erreur
Application
# Soit y la variable dépendante,
# X.bar la pente fixe (moyenne du groupe),
# X.dif l'autre pente fixe (écart individuel à le moyenne de la classe)
# et g le groupe
library(lmerTest)
m <- lmer(y ~ 1 + X.bar + X.dif + (1 + X.dif | g), data=data)
summary(m)
Conditions d'application
Conditions d'application
Comme vu précédemment, pour pouvoir être utilisée, la régression multiniveau requiert (dans le cadre de ce cours):
- Au moins 20 unités au niveau 2 (au moins 20 groupes dans lesquelles sont imbriquées les données).
- La distribution normale des résidus (distribution normale des erreurs).
Pour tester la distribution normale des erreurs, nous pouvons réaliser un graphique Q-Q:
# Soit m le modèle de régression
qqnorm(resid(m))
qqline(resid(m))
Nous pouvons également visualiser la distribution des erreurs dans un histogramme:
# Soit m le modèle de régression
hist(resid(m))
Exemple
Voici nos données et notre fichier d'analyse:
| Fichiers |
|---|
| multilevel-regression-inter-intra-group.csv |
| multilevel-regression-inter-intra-group.R |
Commençons par activer les librairies nécessaires dans R:
library(lmerTest)
library(ggplot2)
library(dplyr)
Puis, importons nos données:
df <- read.csv("multilevel-regression-inter-intra-group.csv")
df$groupe <- as.factor(df$groupe)
Nous devons ensuite trier séparer les effets de groupes des effets individuels:
df1 <- df %>%
group_by(groupe) %>%
mutate(predicteur.bar=mean(predicteur, na.rm=TRUE)) %>%
mutate(predicteur.dif= predicteur - predicteur.bar) %>%
as.data.frame()
Réalisons maintenant notre modèle:
m <- lmer(score ~ predicteur.bar + predicteur.dif
+ (predicteur.dif | groupe), data=df1)
Vérifions ensuite les conditions d'application de la régression:
qqnorm(resid(m))
qqline(resid(m))
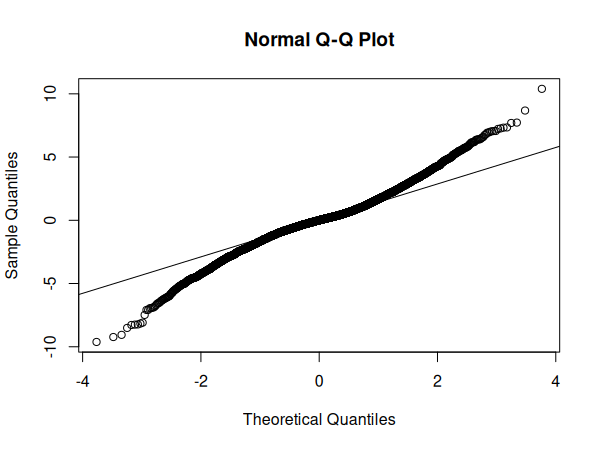
hist(resid(m))
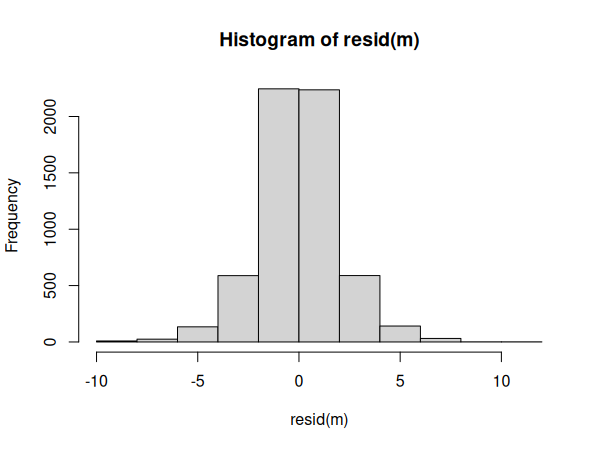
Les conditions semblent remplies, nous pouvons donc passer à l'interprétation des résultats:
summary(m)
Random effects:
| Groups | Name | Variance | Std.Dev | Corr |
|---|---|---|---|---|
| groupe | (Intercept) | 51.212 | 7.156 | |
| predicteur.dif | 8.213 | 2.866 | 0.86 | |
| Residual | 3.828 | 1.957 |
Fixed effects:
| Estimate | Std. Error | df | t value | p | |
|---|---|---|---|---|---|
| (Intercept) | 6.2146 | 2.5033 | 28.3305 | 2.483 | 0.019228 * |
| predicteur.bar | 3.2170 | 0.8061 | 17.9980 | 3.991 | 0.000857 *** |
| predicteur.dif | 3.5006 | 0.6413 | 18.9983 | 5.458 | 2.89e-05 *** |
Correlation of Fixed Effects:
| (Intr) | prdctr.b | |
|---|---|---|
| predictr.br | -0.769 | |
| predictr.df | 0.549 | 0.000 |
Grâce à ces résultats, nous pouvons remarquer que les groupes dans lesquels le prédicteur est plus élevé ont tendance à avoir des scores plus élevés (B = 3.22, p<.001). En outre, au niveau individuel, — après avoir supprimé les influences groupales — les individus pour lesquels le prédicteur est élevé ont tendance à avoir également un score plus élevé (B = 3.50, p<.001). Les effets aléatoires sont ici traités comme des termes d'erreurs — mais ce n'est pas toujours le cas.