Régression multiniveau

Bases théoriques

Dans un modèle multiniveau, les individus sont imbriqués dans des groupes, qui sont eux-encore imbriqués dans des contextes particuliers. Il y a donc plusieurs niveaux. Il n'est donc pas possible d'effectuer une régression simple sur les données, puisque celle-ci nécessite l'indépendance des individus. Or, dans un modèle hiérarchique, les individus sont dépendants des niveaux supérieurs, c'est-à-dire que les différences entre les individus dépendent du groupe de chaque individu, etc.

Si nous pouvions donc représenter la régression simple à l'aide d'une pente:

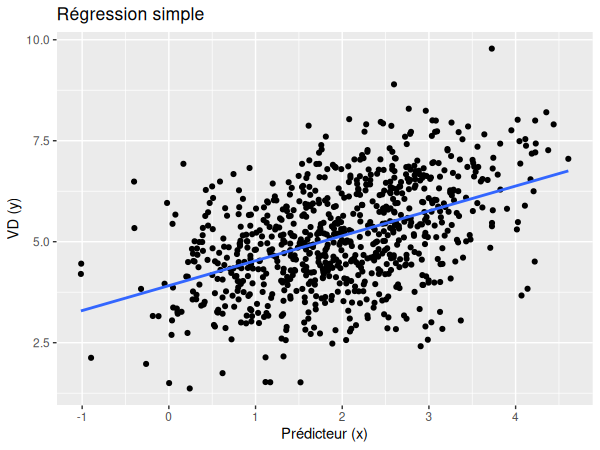
Nous pouvons maintenant prendre en compte les niveaux supérieurs et réaliser plusieurs lignes de régression distinctes:

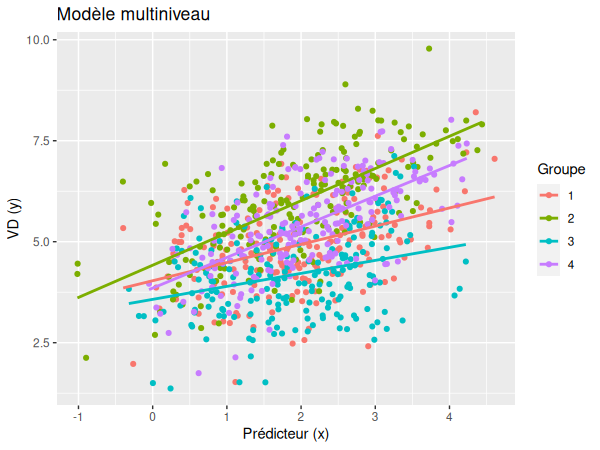
En réalité, les deux sont nécessaire. La pente de régression simple de tous les groupes ensemble est appelée pente fixe et son intercept est appelé intercept fixe. Cela constitue ce que l'on appelle l'effet fixe, car il ne change pas en fonction des groupes. Les pentes pour chaque groupe, elles, s'appellent les pentes aléatoires et leurs intercepts sont nommés intercepts aléatoires, ce qui constitue les effets aléatoires — qui sont différents pour chaque contexte.

L'équation de la régression multiniveau est donc la suivante:

Avec:

• γ₀₀ l'intercept moyenne
• r_0j la déviation spécifique au groupe de l'interception moyenne
• r₁₀ la pente moyenne
• r_1j la déviation spécifique au groupe de la pente moyenne
• ε_ij l'erreur standard de chaque individu par rapport au groupe

Application

# Soit y la variable dépendante, x le prédicteur et g le groupe
library(lmerTest)
m <- lmer(y ~ x + (x | g), data=data)
summary(m)

Conditions d'application

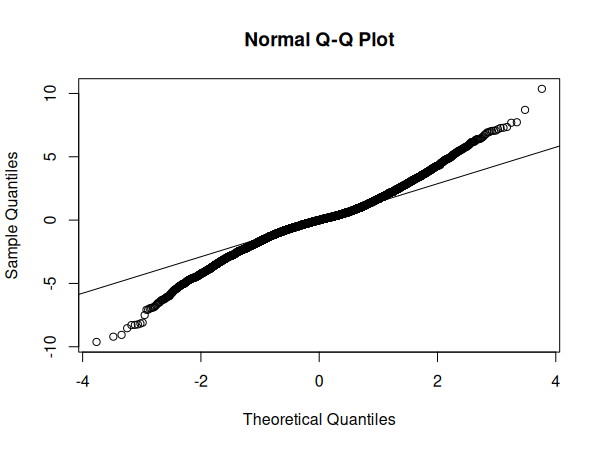
Pour tester la distribution normale des erreurs, nous pouvons réaliser un graphique Q-Q:

# Soit m le modèle de régression
qqnorm(resid(m))
qqline(resid(m))

Nous pouvons également visualiser la distribution des erreurs dans un histogramme:

# Soit m le modèle de régression
hist(resid(m))

Exemple

Voici nos données et notre fichier d'analyse:

Commençons par activer les librairies nécessaires dans R:

library(lmerTest)
library(ggplot2)

Puis, importons nos données:

df <- read.csv("multilevel-regression.csv")
df$groupe <- as.factor(df$groupe)

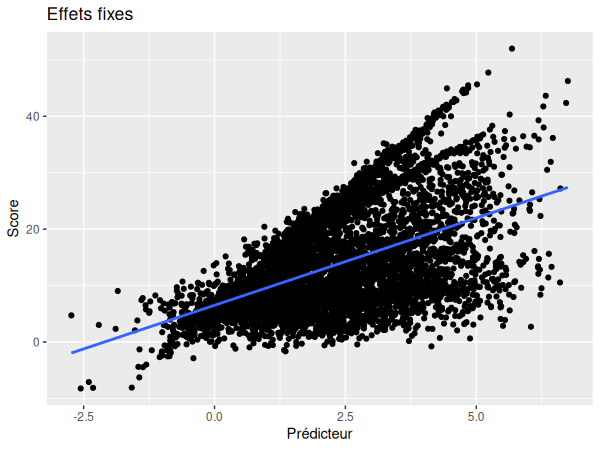
Nous pouvons maintenant visualiser la pente fixe ainsi que les pentes aléatoires:

Effets fixesEffets aléatoires

Représentation graphique des effets fixes

ggplot(data=df, aes(x=predicteur, y=score)) +
  geom_point()+
  geom_smooth(method=lm, se=F) +
  ggtitle("Effets fixes") +
  xlab("Prédicteur") +
  ylab("Score")

Représentation graphique des effets aléatoires

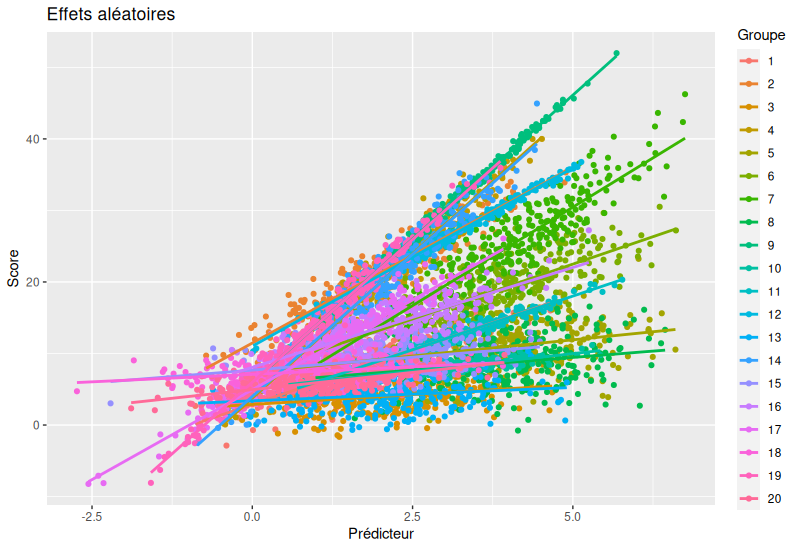
ggplot(data=df, aes(x=predicteur, y=score)) +
  geom_point()+
  geom_smooth(method=lm, se=F) +
  ggtitle("Effets fixes") +
  xlab("Prédicteur") +
  ylab("Score")

Réalisons maintenant notre modèle de régression:

m <- lmer(score ~ predicteur + (predicteur | groupe), data=df)

Nous devons maintenant vérifier les suppositions de notre modèle de régression:

Graphique Q-QHistogramme

Vérification de la normalité des résidus

qqnorm(resid(m))
qqline(resid(m))

Vérification de la normalité des résidus

hist(resid(m))

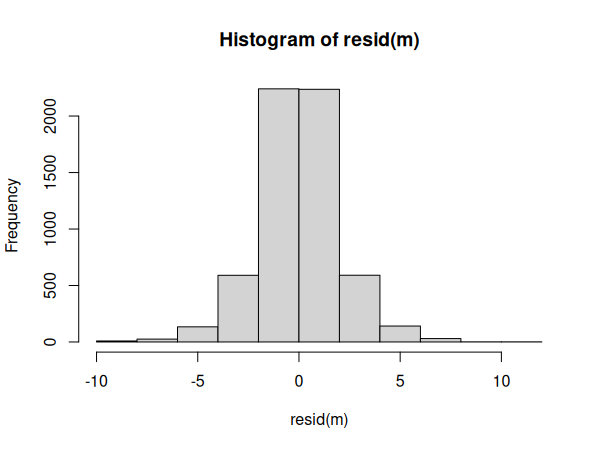
Si le graphique Q-Q ne suit pas tout à fait la ligne centrale, l'histogramme montre toutefois que la distribution des résidus semble parfaitement normale.

Nous pouvons donc passer à l'interprétation des résultats:

summary(m)

Random effects:

Fixed effects: