Modération avec modérateur binaire
Introduction
La modération avec modérateur binaire permet de tester l'effet de prédicteurs qui sont modulés par une variable binaire.
Bases théoriques
Dans le cas de la régression simple, il était possible de représenter graphiquement la ligne de régression de la manière suivante:
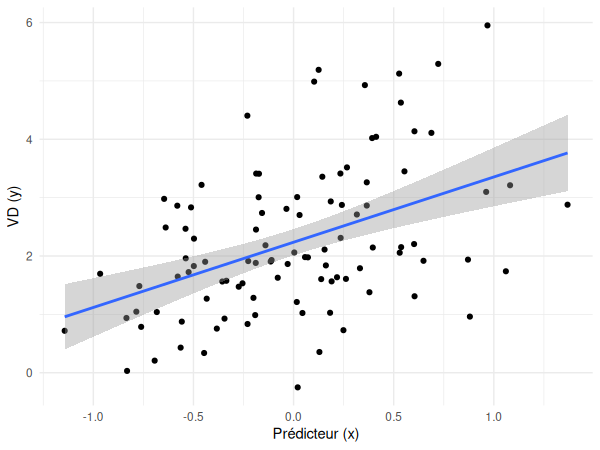
Or, en présence d'un modérateur binaire, l'effet du prédicteur est modulé par la variable modératrice. Il n'y a donc plus une seule pente, mais bien deux (une pour chaque modalité de la variable modératrice), une lorsque z = 0 et l'autre lorsque z = 1 :
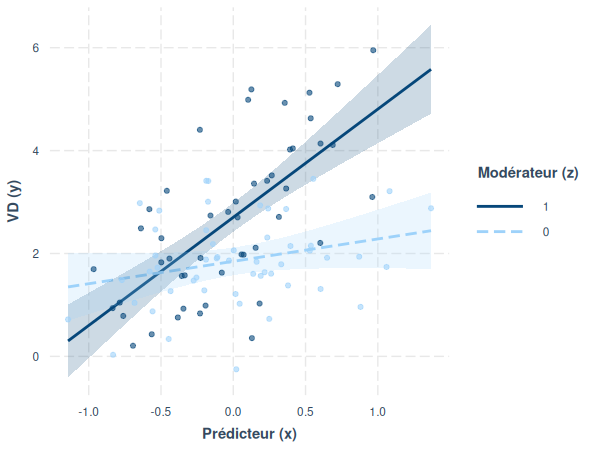
Application
Centrage des prédicteurs numériques
Avant de pouvoir calculer notre modération, il est nécessaire de centrer notre prédicteur numérique (faire en sorte que sa moyenne soit égale à 0). Cela permet de rendre l'interprétation plus pertinente. Le centrage se fait de la façon suivante:
# Soit y la variable dépendante, x1 le prédicteur numérique
data$x1.c <- scale(data$x1, scale=FALSE)
# Soit y la variable dépendante, x1.c le prédicteur numérique centré
# et x2 le modérateur binaire
m <- lm(data$y ~ data$x1.c*data$x2)
summary(m)
Lorsque l'interaction est significative, il est possible de l'interpréter (c'est-à-dire obtenir la valeur des deux pentes) de la façon suivante:
# Soit m le modèle de régression linéaire, x1.c le prédicteur numérique centré
# et x2 le modérateur binaire
library(interactions)
sim_slopes(m1, pred=x1.c, modx=x2)
Conditions d'application
Conditions d'application
Comme pour la régression linéaire multiple, la modération requiert:
- La linéarité du modèle.
- La distribution normale des résidus.
- L'homoscédasticité (constance de la variance des résidus à tous les niveaux du prédicteur).
- L'absence de valeurs extrêmes.
- L'absence de multicolinéarité (absence de corrélation forte entre 2 prédicteurs ou plus).
Comme pour la régression simple, nous pouvons vérifier les 4 premières suppositions de la façon suivante:
# Soit m le modèle linéaire
par(mfrow=c(1,1))
plot(m)
Pour tester la multicolinéarité, nous utilisons le GVIF (Generalized Variance Inflation Factor):
Quelle valeur examiner ?
Dans un modèle contenant des termes d'interaction, il faut examiner la valeur de GVIF^(1/(2*Df)). Il s'agit de la valeur du GVIF ajusté aux degrés de liberté.
# Soit m le modèle linéaire
library(car)
vif(m, type="predictor")
Taille d'effet
Comme dans le cadre d'une régression multiple, nous utilisons le R2 ajusté pour déterminer la part de la variance qui peut être expliquée par l'ensemble de nos prédicteurs.
Exemple
Voici nos données et notre fichier d'analyse:
| Fichiers |
|---|
| binary-moderation.csv |
| binary-moderation.R |
Commençons par activer les librairies nécessaires dans R:
library(car)
library(interactions)
Puis, importons nos données:
df <- read.csv("binary-moderation.csv")
Nous devons ensuite centrer notre prédicteur numérique:
df$predicteur.c <- scale(df$predicteur, scale=FALSE)
Réalisons maintenant notre modèle linéaire:
m <- lm(score ~ predicteur.c * maladie, data=df)
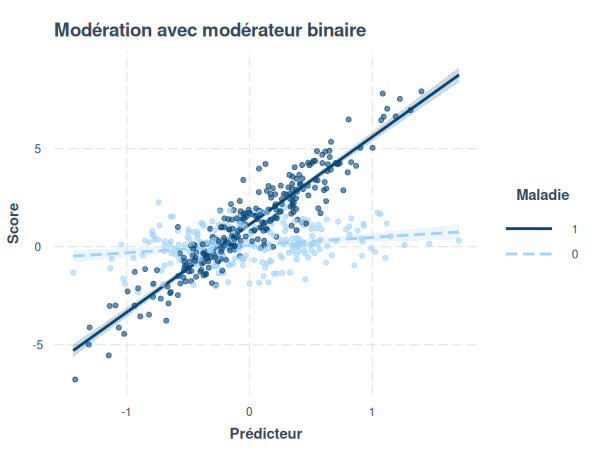
Nous pouvons maintenant visualiser nos données dans un diagramme:
interact_plot(
m, pred=predicteur.c,
modx=maladie, plot.points=TRUE,
interval=TRUE, y.label="Score",
x.label="Prédicteur",
legend.main="Maladie",
main.title="Modération avec modérateur binaire"
)
Nous devons maintenant vérifier les suppositions de notre modération:
par(mfrow=c(1,1))
plot(m)
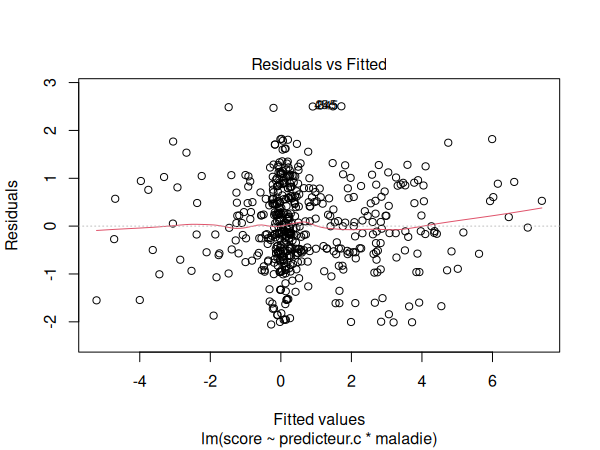
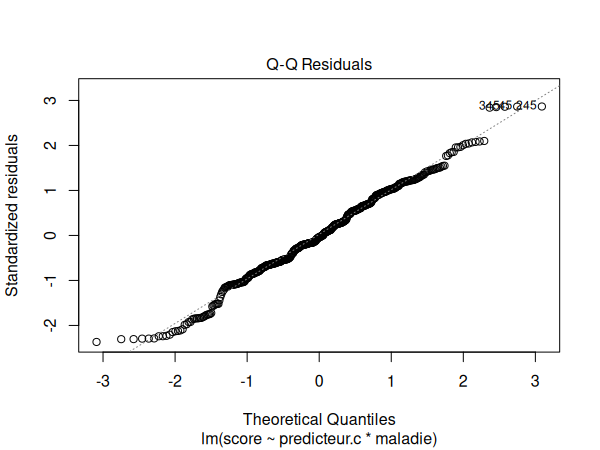
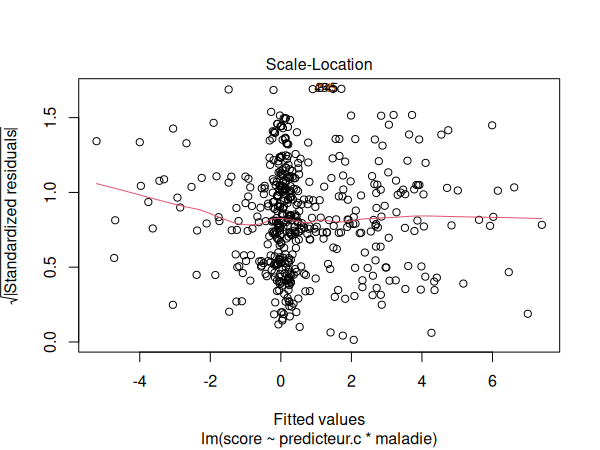
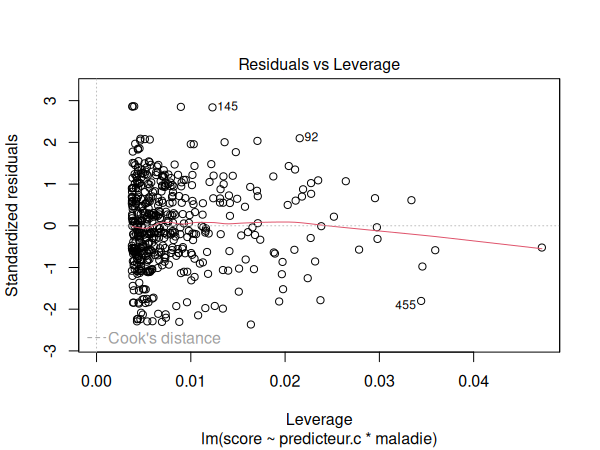
Le graphique de localisation d'échelle est légèrement courbé vers le haut à gauche, mais il s'agit toutefois d'un résultat acceptable.
Puis nous testons notre modèle pour la multicolinéarité:
vif(m, type="predictor")
| GVIF | Df | GVIF^(1/(2*Df)) | Interacts With | Other Predictors | |
|---|---|---|---|---|---|
| predicteur.c | 1 | 3 | 1 | maladie | -- |
| maladie | 1 | 3 | 1 | predicteur.c | -- |
Les suppositions semblent être respectées. Nous pouvons donc interpréter nos résultats:
summary(m)
| Estimate | Std. Error | t value | p | |
|---|---|---|---|---|
| (Intercept) | 0.08194 | 0.05738 | 1.428 | 0.153929 |
| predicteur.c | 0.39226 | 0.10622 | 3.693 | 0.000246 *** |
| maladie | 1.05014 | 0.07853 | 13.373 | <2e-16 *** |
| predicteur.c:maladie | 4.08239 | 0.15137 | 26.970 | <2e-16 *** |
| F-statistic | p-value | Multiple R2 | Adjusted R2 |
|---|---|---|---|
| 639.2 | < 2.2e-16 | 0.7945 | 0.7933 |
Nous voulons ensuite connaître les valeurs des pentes dans les différentes modalités de notre modérateur binaire maladie:
sim_slopes(m, pred=predicteur.c, modx=maladie)
| moderator | Est. | S.E. | t val. | p |
|---|---|---|---|---|
| maladie = 0 | 0.39 | 0.11 | 3.69 | 0.00 |
| maladie = 1 | 4.47 | 0.11 | 41.49 | 0.00 |
Nous pouvons déduire de ces résultats que nos prédicteurs sont significatifs et qu'ils permettent d'expliquer ~79% de la variance des scores (F(3,496) = 639.2, p<.001, R2 = .793). Le prédicteur a un effet significatif sur le score (B = 0.39, p<.001) ainsi qu'un effet d'interaction avec la présence ou non de maladie (B = 4.08, p<.001).
Une augmentation d'une unité du prédicteur lorsque le sujet n'est pas malade (maladie = 0) est associée à une augmentation moyenne de 0.39 unités du score (B = 0.39, t(496) = 3.69, p<.001). Une augmentation d'une unité du prédicteur lorsque le sujet est malade (maladie = 1) est associée à une augmentation moyenne de 4.47 unités du score (B = 4.47, t(496) = 41.49, p<.001).