Coefficient de corrélation ρ de Spearman (Spearman's Rho)
Introduction
Le coefficient de corrélation ρ de Spearman permet de décrire la corrélation entre deux variables, dont au moins l'une est continue. Il est l'équivalent non-paramétrique du coefficient de corrélation r de Pearson.
Conditions d'application
Conditions d'application
Pour pouvoir être appliqué, cette analyse nécessite que les échantillons ne soient pas issues de distributions normales.
- Si les distributions sont normales, il faut absolument utiliser son équivalent paramétrique. Dans ce cas, le coefficient r de Pearson.
Pour vérifier si les distributions sont normales, nous devons utiliser un test de Shapiro-Wilk:
# Soient X1 et X2 nos deux variables
shapiro.test(data$X1)
shapiro.test(data$X2)
Application
# Soit X1 et X2 nos deux variables
library(Hmisc)
rcorr(
as.matrix(data[,c("X1","X2")]),
type="spearman"
)
Exemple
Voici nos données et notre fichier d'analyse:
| Fichiers |
|---|
| spearman-rho.csv |
| spearman-rho.R |
Commençons par activer les librairies nécessaires dans R:
library(ggplot2)
library(Hmisc)
library(outliers)
Puis, importons nos données:
df <- read.csv("spearman-rho.csv")
Nous pouvons maintenant visualiser nos données dans un diagramme en points:
ggplot(df, aes(x=score_1, y=score_2)) +
geom_point() +
geom_smooth() +
xlab("Score 1") +
ylab("Score 2") +
ggtitle("Speaman's rho")
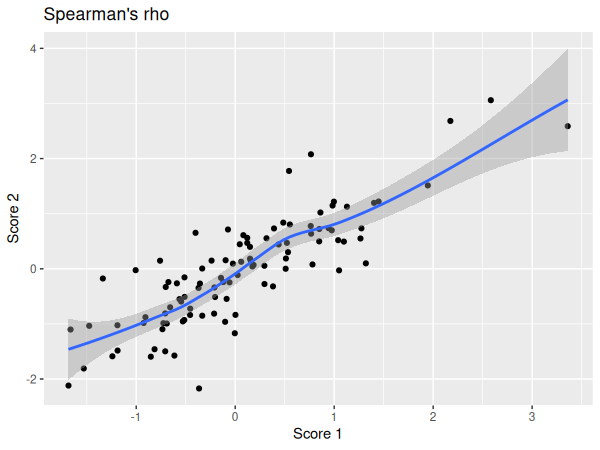
Vérifions maintenant la normalité des distributions:
shapiro.test(df$score_1)
shapiro.test(df$score_2)
| W | p | |
|---|---|---|
| Score 1 | 0.96873 | 0.01769 |
| Score 2 | 0.97677 | 0.07431 |
Nous pouvons donc conclure que l'un de nos échantillon n'est pas issu d'une distribution normale. Nous devons donc réaliser une analyse non-paramétrique:
rcorr(
as.matrix(df[,c("score_1", "score_2")]),
type="spearman"
)
| Score 1 | Score 2 | |
|---|---|---|
| Score 1 | 1.00 | 0.84 |
| Score 2 | 0.84 | 1.00 |
| n |
|---|
| 100 |
| P | Score 1 | Score 2 |
|---|---|---|
| Score 1 | 0 | |
| Score 2 | 0 |
Nous pouvons donc conclure qu'il existe une corrélation entre nos deux variables, et que celle-ci est forte.