Coefficient de corrélation r de Pearson (Pearson's r)

Introduction

Le coefficient de corrélation r de Pearson permet de décrire la corrélation entre deux variables numériques.

Conditions d'application

Pour pouvoir être appliqué, cette analyse nécessite que les échantillons soient issus de distributions normales et qu'ils ne contiennent pas de valeurs extrêmes.

Si les échantillons ne proviennent pas de distribution normales, il faut utiliser son équivalent non-paramétrique. Dans ce cas, le coefficient ρ de Spearman.
Si des valeurs extrêmes sont présentes, il faut utiliser une correction, dans ce cas le coefficient τ de Kendall (pas important pour ce cours).

Pour vérifier si les distributions sont normales, nous devons utiliser un test de Shapiro-Wilk:

Syntaxe R

# Soient X1 et X2 nos deux variables
shapiro.test(data$X1)
shapiro.test(data$X2)

Puis, pour vérifier si les échantillons contiennent des valeurs extrêmes, nous devons utiliser un test de Grubbs:

Syntaxe R

# Soient X1 et X2 nos deux variables
library(outliers)
grubbs.test(data$X1)
grubbs.test(data$X2)

Application

Avec R

Syntaxe R

# Soit X1 et X2 nos deux variables
library(Hmisc)
rcorr(
    as.matrix(data[,c("X1","X2")]),
    type="pearson"
)

Interprétation

Selon la convention fixée par Cohen, nous pouvons interpréter la force de la corrélation de la manière suivante:

0.1 ≤ r < 0.3	0.3 ≤ r < 0.5	0.5 ≤ r
Faible	Moyenne	Forte

Exemple

Voici nos données et notre fichier d'analyse:

Fichiers
pearson-r.csv
pearson-r.R

Commençons par activer les librairies nécessaires dans R:

Activation des librairies

library(ggplot2)
library(Hmisc)
library(outliers)

Puis, importons nos données:

Importation des données

df <- read.csv("pearson-r.csv")

Nous pouvons maintenant visualiser nos données dans un diagramme en points:

Diagramme en points

ggplot(df, aes(x=score_1, y=score_2)) +
    geom_point() +
    geom_smooth() +
    xlab("Score 1") +
    ylab("Score 2") +
    ggtitle("Pearson's r")

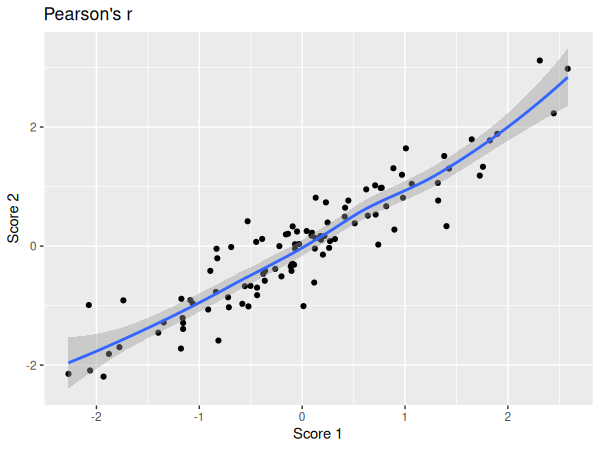
Vérifions maintenant la normalité des distributions:

Test de normalité de Shapiro-Wilk

shapiro.test(df$score_1)
shapiro.test(df$score_2)

	W	p
Score 1	0.98836	0.535
Score 2	0.98608	0.379

Nous pouvons donc conclure que les deux échantillons sont issus de distributions normales.

Testons maintenant si des valeurs extrêmes sont présentes:

Test de Grubbs pour les valeurs extrêmes

grubbs.test(df$score_1)
grubbs.test(df$score_2)

	G	U	p
Score 1	2.52672	0.93486	0.5192
Score 2	2.97752	0.90954	0.1181

Nous pouvons conclure qu'il n'existe pas de valeurs extrêmes dans nos échantillons.

Puisque les conditions d'applications sont respectées, nous pouvons donc réaliser notre analyse paramétrique.

Coefficient de corrélation r de Pearson

rcorr(
  as.matrix(df[,c("score_1", "score_2")]),
  type="pearson"
)

	Score 1	Score 2
Score 1	1.00	0.93
Score 2	0.93	1.00

n
100

P	Score 1	Score 2
Score 1		0
Score 2	0

Nous pouvons donc conclure qu'il existe une corrélation entre nos deux variables, et que celle-ci est forte.