Test de Welch sur deux échantillons indépendants (Welch two sample t-test)

Introduction

La correction de Welch permettet d'effectuer un t-test à deux échantillons indépendants sur des échantillons dont les variances ne sont pas homogènes.

Pour des explications plus détaillées, n'hésitez pas à consulter mes notes de première année.

Conditions d'application

Pour pouvoir être appliqué, ce test nécessite que les échantillons soient issus de distributions normales et que leurs variances ne soient pas homogènes.

Si les échantillons ne proviennent pas de distribution normales, il faut utiliser un test non-paramétrique. Dans ce cas, un test de Mann-Whitney.
Si les variances sont homogènes, il ne faut surtout pas utiliser de correction. Dans ce cas, il faut utiliser un test de Student.

Pour vérifier si les distributions sont normales, nous devons utiliser un test de Shapiro-Wilk:

Syntaxe R

# Soit y la variable dépendante et x la variable indépendante/manipulée
by(data$y, data$x, shapiro.test)

Pour vérifier si les variances sont homogènes, nous devons utiliser un test de Levene:

Syntaxe R

# Soit y la variable dépendante et x la variable indépendante/manipulée
library(car)
leveneTest(data$y ~ data$x)

Exécution du test

Syntaxe R

# Soit y la variable dépendante et x la variable indépendante/manipulée
t.test(data$y ~ data$x, var.equal=FALSE)

Note

Ici, nous n'aurions en réalité pas besoin d'écrire l'argument var.equal=FALSE puisqu'il s'agit de la valeur par défaut.

Exemple

Voici nos données et notre fichier d'analyse:

Fichiers
welch-two-sample-t-test.csv
welch-two-sample-t-test.R

Commençons par activer les librairies nécessaires dans R:

Activation des librairies

library(car)

Puis, importons nos données:

Importation des données

df <- read.csv("welch-two-sample-t-test.csv")
df$groupe <- as.factor(df$groupe)

Nous pouvons maintenant visualiser nos données dans un diagramme en boîtes à moustache:

Diagramme en boîtes à moustache

boxplot(
    score ~ groupe, data=df,
    xlab="Groupe", ylab="Score",
    main="Two sample t-test",
    col="steelblue"
)

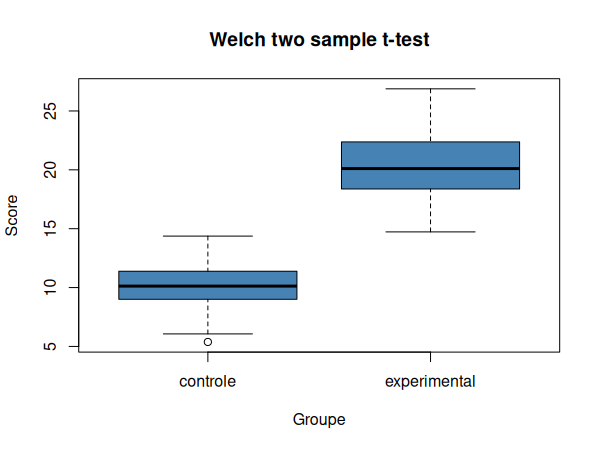
Vérifions maintenant les conditions d'application, tout d'abord la normalité des distributions:

Test de normalité de Shapiro-Wilk

by(df$score, df$groupe, shapiro.test)

	W	p
Contrôle	0.99388	0.9349
Expérimental	0.97604	0.06513

Nous pouvons donc conclure que les deux échantillons sont issus de distributions normales.

Puis, nous vérifions l'homogénéité des variances:

Test d'homogénéité des variances

leveneTest(score ~ groupe, data=df)

	Df	F	Pr(>F)
group	1	15.658	0.0001057 ***
	198

Nous pouvons donc conclure que les variances ne sont pas homogènes. Nous devons donc utiliser la correction de Welch.

Nous pouvons donc maintenant effectuer notre t-test avec correction de Welch:

Test de Welch indépendant

t.test(score ~ groupe, data=df, var.equal=FALSE)

t	df	p
-30.082	168.55	< 2.2e-16 ***

Nous pouvons donc conclure qu'il existe une différence significative entre les deux groupes (t_(168.55) = -30.08, p<.001).