Analyse de moyenne à un facteur (one way analysis of means)
Introduction
L'analyse de moyenne de Welch à un facteur est une correction permettant de réaliser une ANOVA sur des échantillons dont les variances ne sont pas homogènes.
Pour des explications plus détaillées, n'hésitez pas à consulter mes notes de première année.
Conditions d'application
Conditions d'application
Pour pouvoir être appliqué, ce test nécessite que les échantillons soient issus de distributions normales et que leurs variances ne soient pas homogènes.
- Si les échantillons ne proviennent pas de distribution normales, il faut utiliser un test non-paramétrique. Dans ce cas, un test de Kruskal-Wallis.
- Si les variances sont homogènes, il ne faut surtout pas utiliser de correction. Dans ce cas, il faut utiliser une ANOVA à un facteur.
Pour vérifier si les distributions sont normales, nous devons utiliser un test de Shapiro-Wilk:
# Soit y la variable dépendante et x le facteur
by(data$y, data$x, shapiro.test)
Pour vérifier si les variances sont homogènes, nous devons utiliser un test de Levene:
# Soit y la variable dépendante et x le facteur
library(car)
leveneTest(data$y ~ data$x)
Exécution du test
# Soit y la variable dépendante et x le facteur
oneway.test(data$y ~ data$x)
Exemple
Voici nos données et notre fichier d'analyse:
| Fichiers |
|---|
| one-way-analysis-of-means.csv |
| one-way-analysis-of-means.R |
Commençons par activer les librairies nécessaires dans R:
library(car)
Puis, importons nos données:
df <- read.csv("one-way-analysis-of-means.csv")
df$groupe <- as.factor(df$groupe)
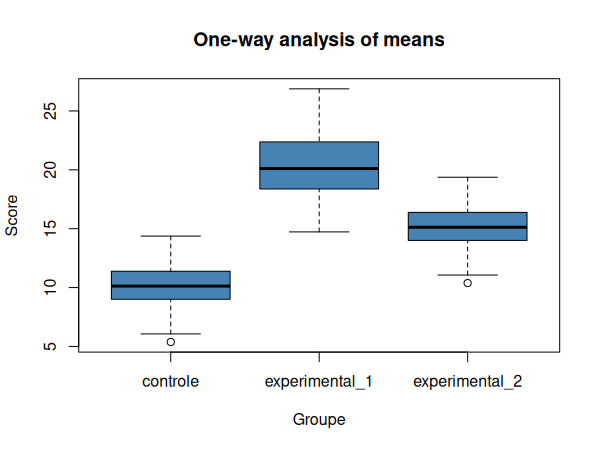
Nous pouvons maintenant visualiser nos données dans un diagramme en boîtes à moustache:
boxplot(
score ~ groupe, data=df,
xlab="Groupe", ylab="Score",
main="One-way analysis of means",
col="steelblue"
)
Vérifions maintenant les conditions d'application, tout d'abord la normalité des distributions:
by(df$score, df$groupe, shapiro.test)
| W | p | |
|---|---|---|
| Contrôle | 0.99388 | 0.9349 |
| Expérimental 1 | 0.97604 | 0.06513 |
| Expérimental 2 | 0.99388 | 0.9349 |
Nous pouvons donc conclure que tous les échantillons sont issus de distributions normales.
Puis, nous vérifions l'homogénéité des variances:
leveneTest(score ~ groupe, data=df)
| Df | F | Pr(>F) | |
|---|---|---|---|
| group | 2 | 12.191 | 8.157e-06 *** |
| 297 |
Nous pouvons donc conclure que les variances ne sont pas homogènes. Nous devons donc utiliser la correction de Welch.
Réalisons maintenant notre analyse de moyenne à un facteur
oneway.test(score ~ groupe, data=df)
| F | num df | denom df | p-value |
|---|---|---|---|
| 487.21 | 2.00 | 192.25 | < 2.2e-16 *** |
Nous constatons donc qu'il existe un effet significatif des différentes modalités de notre facteur groupe (F~(2, 192.25)~ = 487.21, p<.001).