Test de normalité de Shapiro-Wilk (Shapiro-Wilk normality test)
Introduction
Le test de normalité de Shapiro-Wilk est un test statistique permettant de vérifier si une distribution est normale.
Exécution du test
Syntaxe R
# Soit y la variable dépendante et x la variable indépendante/manipulée
by(data$y, data$x, shapiro.test)
Syntaxe R
# Soit Y un vecteur de nos observations
shapiro.test(Y)
Interprétation
| p >= 0.05 | p < 0.05 * |
|---|---|
| Acceptation de l'hypothèse nulle. | Rejet de l'hypothèse nulle. |
| La distribution est normale. | La distribution n'est pas normale. |
Exemple
Voici nos données et notre fichier d'analyse:
| Fichiers |
|---|
| shapiro-wilk-normality-test.csv |
| shapiro-wilk-normality-test.R |
Importons nos données:
Importation des données
df <- read.csv("shapiro-wilk-normality-test.csv")
Nous allons tester deux distributions pour voir si celles-ci sont normales.
Nous pouvons visualiser nos données dans un histogramme:
Histogramme
hist(
df$score_1,
col="pink",
xlab="Score 1",
ylab="Fréquence",
main="Shapiro-Wilk normality test"
)
hist(
df$score_2,
col="pink",
xlab="Score 2",
ylab="Fréquence",
main="Shapiro-Wilk normality test"
)
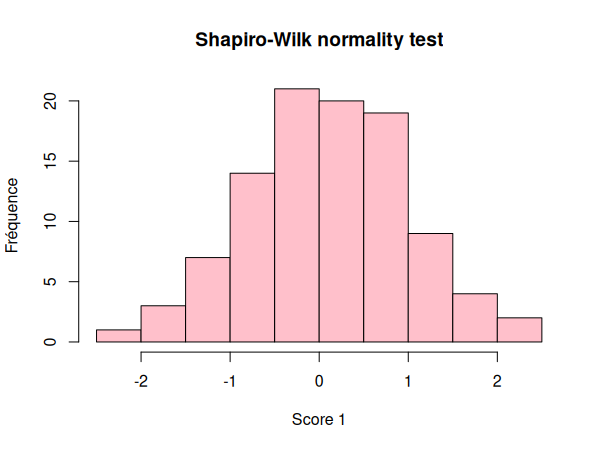
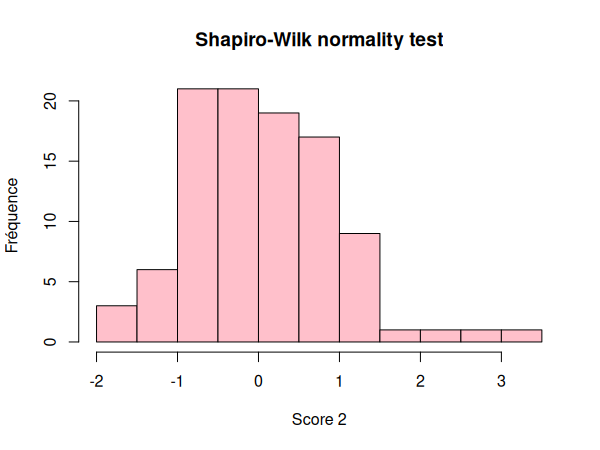
Nous pouvons maintenant réaliser notre test de normalité des distributions:
Test de normalité de Shapiro-Wilk
shapiro.test(df$score_1)
shapiro.test(df$score_2)
| W | p | |
|---|---|---|
| Score 1 | 0.9956 | 0.9876 |
| Score 2 | 0.96873 | 0.01769 |
Nous pouvons donc conclure que l'échantillon score_1 est issu d'une distribution normale, et que score_2 ne l'est pas.