Test d'homogénéité des variances de Levene (Levene's test for homogeneity of variance)
Introduction
Le test d'homogénéité des variances de Levene est un test statistique permettant de vérifier si les variances de plusieurs échantillons sont homogènes.
Exécution du test
Syntaxe R
# Soit y la variable dépendante et x la variable indépendante/manipulée
library(car)
leveneTest(data$y ~ data$x)
Interprétation
| p >= 0.05 | p < 0.05 * |
|---|---|
| Acceptation de l'hypothèse nulle. | Rejet de l'hypothèse nulle. |
| Les variances sont homogène. | Les variances ne sont pas homogène. |
Exemple
Voici nos données et notre fichier d'analyse:
| Fichiers |
|---|
| levene-test-for-homogeneity-of-variance.csv |
| levene-test-for-homogeneity-of-variance.R |
Commençons par activer les librairies nécessaires dans R:
Activation des librairies
library(car)
Importons nos données:
Importation et recodage des données
data <- read.csv("levene-test-for-homogeneity-of-variance.csv")
df <- data.frame(
score=c(data$score_1, data$score_2),
groupe=factor(rep(c(1, 2), each=100))
)
Nous allons tester deux distributions pour voir si les variances de celles-ci sont homogènes.
Nous pouvons visualiser nos données dans un diagramme en boîtes à moustache:
Diagramme en boîtes à moustache
boxplot(df$score ~ df$groupe)
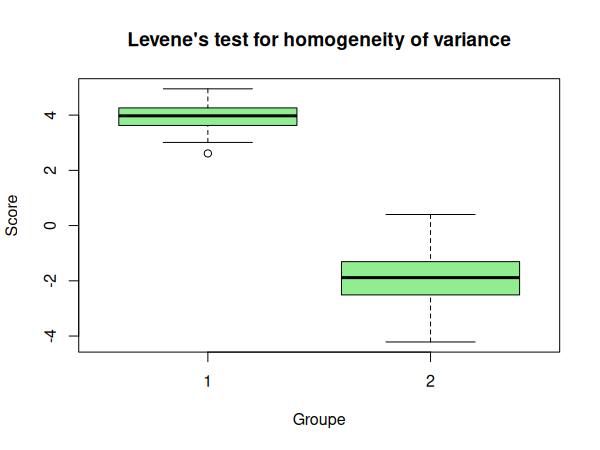
Nous pouvons maintenant réaliser notre test d'homogénéité des variances:
Test d'homogénéité des variances de Levene
leveneTest(df$score ~ df$groupe)
| Df | F | Pr(>F) | |
|---|---|---|---|
| group | 1 | 31.14 | 7.824e-08 *** |
| 198 |
Nous pouvons donc conclure que les variances de nos échantillons ne sont pas homogènes.